Preferably a Holocene colander?
A consensus view was formally adopted by the IUGS in 2013, placing its start at 11,700 years before 2000 (9701 BC), about 300 years more recent than the epoch of the Holocene calendar.[6]
Some problems with Gregorian calendar
The Gregorian calendar improves the approximation made by the Julian calendar by skipping three Julian leap days in every 400 years, giving an average year of 365.2425 mean solar days long.[82] This approximation has an error of about one day per 3,030 years[s] with respect to the current value of the mean tropical year. However, because of the precession of the equinoxes, which is not constant, and the movement of the perihelion (which affects the Earth’s orbital speed) the error with respect to the astronomical vernal equinox is variable; using the average interval between vernal equinoxes near 2000 of 365.24237 days[83] implies an error closer to 1 day every 7,700 years. By any criterion, the Gregorian calendar is substantially more accurate than the 1 day in 128 years error of the Julian calendar (average year 365.25 days).
In the 19th century, Sir John Herschel proposed a modification to the Gregorian calendar with 969 leap days every 4,000 years, instead of 970 leap days that the Gregorian calendar would insert over the same period.[84] This would reduce the average year to 365.24225 days. Herschel’s proposal would make the year 4000, and multiples thereof, common instead of leap. While this modification has often been proposed since, it has never been officially adopted.[85]
On time scales of thousands of years, the Gregorian calendar falls behind the astronomical seasons. This is because the Earth’s speed of rotation is gradually slowing down, which makes each day slightly longer over time (see tidal acceleration and leap second) while the year maintains a more uniform duration.
Calendar seasonal error Gregorian calendar seasons difference
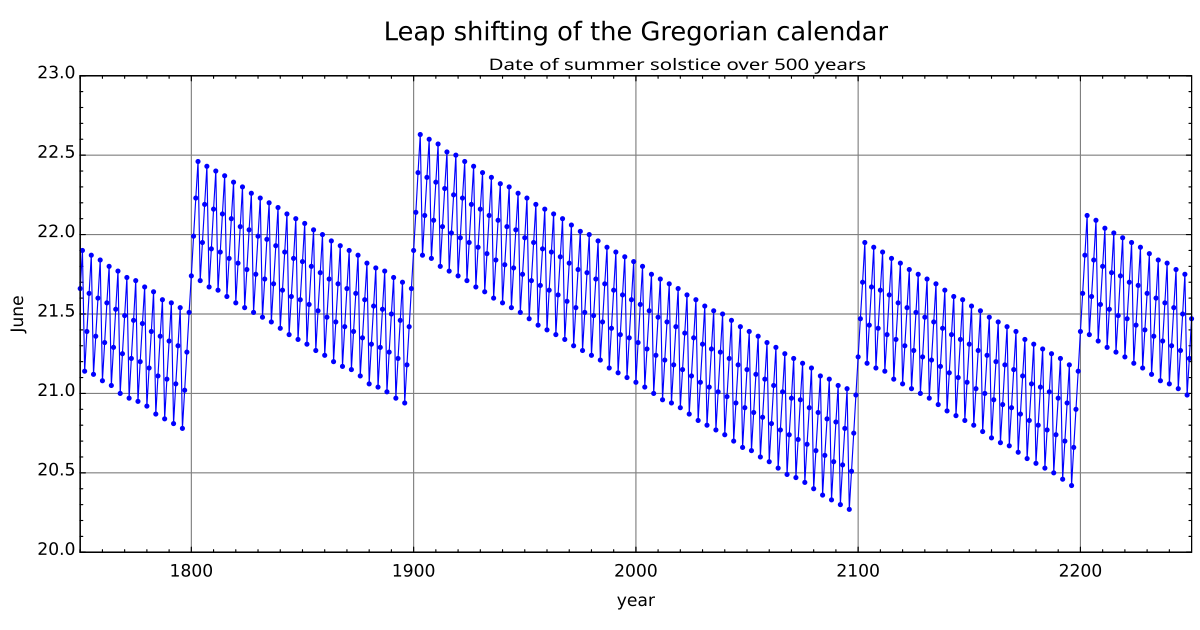
This image shows the difference between the Gregorian calendar and the astronomical seasons.
The y-axis is the date in June and the x-axis is Gregorian calendar years.
Each point is the date and time of the June solstice in that particular year. The error shifts by about a quarter of a day per year. Centurial years are ordinary years, unless they are divisible by 400, in which case they are leap years. This causes a correction in the years 1700, 1800, 1900, 2100, 2200, and 2300.
For instance, these corrections cause 23 December 1903 to be the latest December solstice, and 20 December 2096 to be the earliest solstice—about 2.35 days of variation compared with the astronomical event.
Proposed reforms The following are proposed reforms of the Gregorian calendar:
Holocene calendar
International Fixed Calendar (also called the International Perpetual calendar)
World Calendar
World Season Calendar
Leap week calendars
Pax Calendar
Symmetry454
Hanke–Henry Permanent Calendar


“Day” and “year” have local equivalents for any orbiting, revolving body. We’d probably retain the second as the basic unit of time and maybe go to something like decimal time as a generic standard for communicating between places and for trade and business. That covers spans of time. For absolute time, we may be out of luck. Even assuming we could pick a standard object and point in time as anchors, relativity means that each frame of reference has clocks moving at their own speeds. So far as we know, there is no universal frame of reference.
So even if we said “every revolution of the pulsar at coordinates blahblahblah is one galactic standard day and we define Year 0 as starting exactly 3237.95 standard days ago” we still wouldn’t have a universal time standard because people close to black holes will have seen fewer rotations of the pulsar, so they’d be living in the pasts of any planets in a faster frame of reference.
It’s not hard to keep clocks ‘synchronized’. the GPS system relies on being kept synchronized very precisely, despite being a couple dozen or so clocks that are constantly moving through their own inertial frames. (remember, GPS works by knowing the precise position of the satellites, and them broadcasting a time-stamped message. You then use that to determine how long the message took, and their relative times from at least three of them to pinpoint your place on the surface.)
It’s not like they have to be quantum entangled or whatever so that they’re constantly reporting the exact same time. For industrial, commercial, and social purposes… fudging things by adding ‘make up time’ into a local day (or subtracting it,) to keep weeks and months in sync are “good enough”, and for scientific purposes requiring exactitudes, well, there’s solutions there.